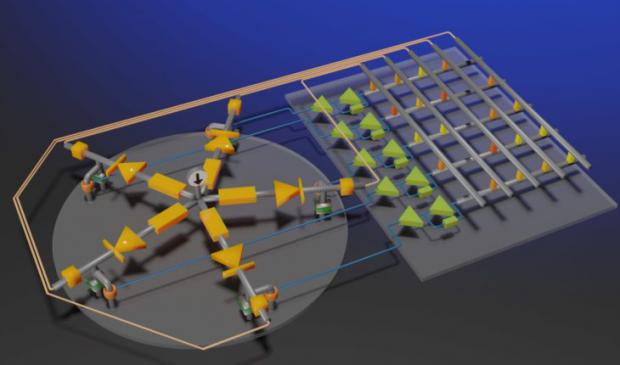
The salesman problem is this question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?". Having really good solutions for this class of problems means the US postal service, Fedex, UPS, airlines and the US military would save huge amounts of money. It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

Conventional digital computers, including supercomputers, are inadequate to solve these complex problems in practically permissible time as the number of candidate solutions they need to evaluate increases exponentially with the problem size. This is a combinatorial explosion. D-Wave Systems and others have created "Ising machines" and "quantum annealers," have been actively developed in recent years. There is complicated pre-processing to convert each task to the form they can handle and have a risk of presenting illegal solutions that do not meet some constraints and requests, resulting in major obstacles to the practical applications.

Approximation Algorithms

Various heuristics and approximation algorithms, which quickly yield good solutions, have been devised. These include the Multi-fragment algorithm. Modern methods can find solutions for extremely large problems (millions of cities) within a reasonable time which are with a high probability just 2–3% away from the optimal solution.

Exact algorithms
The most direct solution would be to try all permutations (ordered combinations) and see which one is cheapest (using brute-force search). The running time for this approach lies within a polynomial factor of {displaystyle O(n!)}O(n!), the factorial of the number of cities, so this solution becomes impractical even for only 20 cities.